▼
ランベルト・ベールの法則の概要
紫外可視吸収分光法を通して必ず学ぶ法則がランベルト・ベールの法則である。分光分析において最も広く利用される定量法には欠かせない法則です。
物質が電磁波を吸収する場合には，電磁波の種類に関係なく成立する定量法です。
A = ε × ｃ × ℓ (式1)
Aを吸光度，モル吸光係数を ε, 吸光物質の濃度をｃ(mol/L)，セル容器の光路長を ℓ (m)とする。
センチの光学セルを用いることが多いため，モル吸光係数の単位は(mol/L)-1cm-1が良く用いられます。
さらには，たいていの実験において光路長1cmのセルを用います。
モル吸光係数は物質固有の定数なので，吸光度(A)と濃度(c)に比例関係があることがわかります。
つまり，物質の吸収する度合い(吸光度)から物質の濃度を算出することができます。
ランベルト・ベールの法則の導出を通して，本法則の限界(吸光度の最適値)を考えてみましょう。
ランベルト・ベールの法則の導出
▼
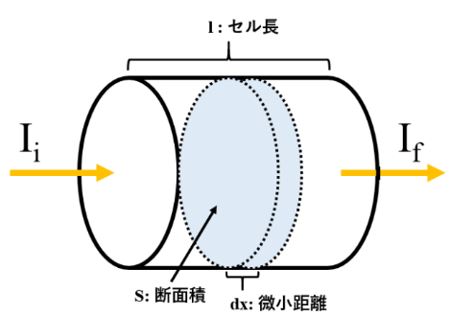
測定物質溶液を入れた測定セルに所望の光をあてます。入射光の強度(Ii)に対する透過光の強度(If)により測定物質の吸光度を測定する。
光が通過する微小体積(断面積×微小距離；S × dx)に含まれる測定対象物の分子数は，アボガドロ数NAとモル濃度ｃから，
分子数 = NA × ｃ × Ｓ × dx (式2)
となります。
測定対象物は独立に光を吸収すると仮定して，測定対象物の吸収断面積(σ)を考慮すると，式(２)から式(３)が導かれる。
分子に吸収される光 = σ × NA × ｃ × Ｓ × dx (式３)
【重要な仮定】粒子に独立に光を当てる
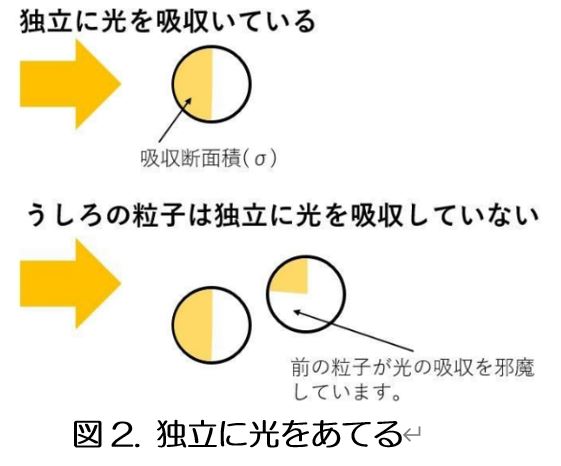
吸光度の最適値を考慮する上で，独立に光を吸収するという仮定がとても重要になる。
図２から「独立に光を吸収するというイメージ」がわかると思います。
独立に入射光が測定物質にあたることにより，入射光と測定物質が相互作用して，透過光として減衰した光が出てきます。
図２の下側の例のように，前の粒子によって，光を受ける吸収断面積が小さく見積もられると，σが小さくなります。
結果，吸光度が低く見積もられ濃度が低い値(誤差)になります。
単位断面積Sあたりの光が測定対象物に吸収される割合は式３から式４が導かれます。
単位断面積の光の吸収割合＝ (σ×NA×c×S×dx)/S = σ×NA×c×dx (式４)
微小距離dxを進む間の光強度の変化量(－dI)は，入射光の強度 I(in) と単位面積当たりの光の吸収割合(式４)に比例するので，
-dI = I(in) ×σ×NA×c×S×dx (式５)
式５を変形して，式６を導きます。
-dI /(I(in)) = σ×NA×c×S×dx (式６)
微小距離ｘ＝０の時，入射光 I(i) とする。微小距離ｘ＝ℓ の時，透過光 I(f) とする。式1.9を上記の範囲(0～ｘ～ ℓ)で積分すると以下のようになります。
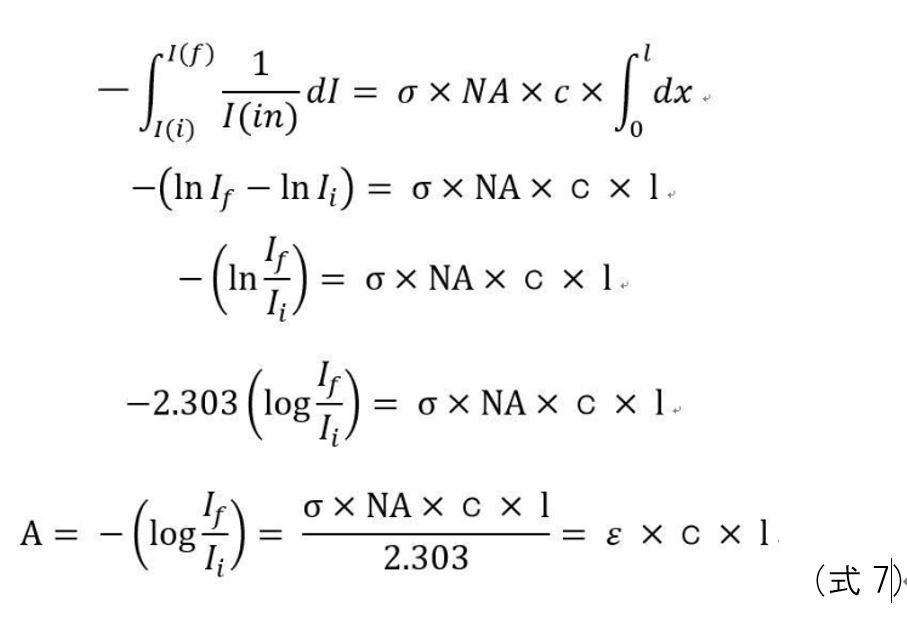
最終的には，式7のランベルト・ベールの法則が導かれました。
モル吸光係数が，物質固有の値である吸収断面積(σ)とアボガドロ数から成立していることもわかります。
吸光度の最適値は？
結論から，吸光度の最適値は0.3以下であり，最高の値は1.0以下であることが望ましい。これは，上記の式７に数値を代入して考えるとスグにわかる。
ポイントは，「独立に光を吸収する」という仮定のもと成立している式ということです。
・吸光度Aが 1.0の場合
吸光度Aに１．０を代入した（式7）を考えてみます。
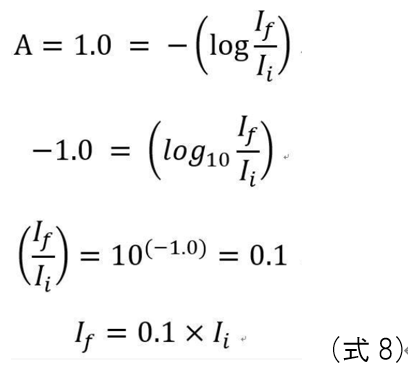
吸光度Aが１．０の場合，入射光(I(i))の０．１倍が透過光(I(f))と式から読み取れます。つまり，入射光の90％が吸収されて，入射光の0.1倍つまり10％程度が透過光として検出されたことを意味しています。
入射光に対して，10％しか透過光として出てこない条件を【独立した光を吸収】と言えるのかを考えてみましょう。
独立に光を吸収できるかどうかは，測定対象物の量が関係してくることがわかるかと思います。測定対象物の量(=濃度)を下げることで，測定物質が独立に光を吸収できる確率を上げることができます。
より具体的には，吸光度が０．３の場合を考えると「グット」わかります。
・吸光度Aが 0.3の場合
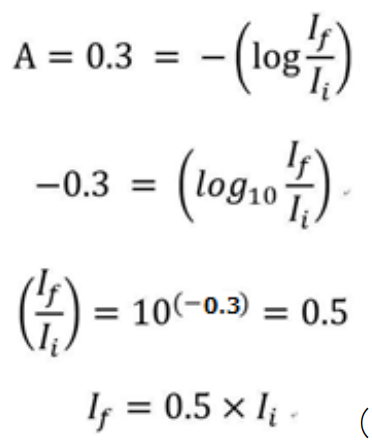
吸光度Aが0.3の場合，入射光 I(i) の0.5倍，つまり50％が透過光 I(f) として検出される計算になります。吸光度Aが1.0の10％しか透過光が出てこない【吸光度Aが1.0の】条件に比べて，50％も透過光が出てくる条件であれば【測定物質が独立に光を吸収】していると考えられます。
この理由から，吸光度は0.3が最適であり，吸光度は最高でも0.1ぐらいが最高だと結論付けることができます。
なお，吸光度Aが「２．０」の場合，入射光の「１％」しか透過光として出てきません。１％しか出てこない溶液の濃さでは，光が測定物質に「独立」に光を浴びているかどうかは疑わしいものです。
